Topic: Equilibrium of Force Systems and Wind Loads
Subject: Fluid and Engineering Mechanics
Tool: QCAD & Scilab
- Gantry Crane Structure and Equilibrium of Force Systems
Gantry cranes are travelling cranes designed for lifting and moving heavy loads. This material handling equipment is generally used outdoors where it is not convenient to erect an overhead runway. Its structure consists of a girder or bridge, freestanding legs, electric motor that drives the steel wheel, and a rail system on the ground. The bridge or girder is carried at the ends by the legs supported by trucks with wheels so that the crane can travel. The bridge carries a hoisting assembly unit. The crane is driven by the motor through a gear reduction shaft. [1]. The motor is referred to as a brake motor because it prevents movement caused by inertia when it is deenergized.
The objective of this article is to present an engineering simulation method of analyzing the effect of a wind loads due to typhoon to an outdoor gantry crane. The assumption is that there is a particular value of wind velocity that will make the crane to tip over at the wind direction.
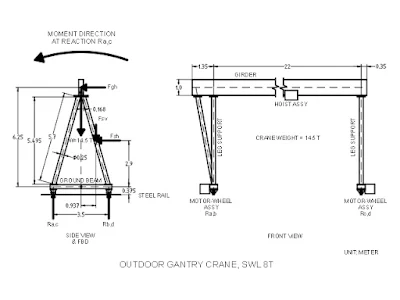
Figure 1 shows a simple illustration of an outdoor gantry crane. On its side view is the free-body diagram (FBD) showing the corresponding concurrent forces acting on the structure. The following conventions will be used in the analysis: - \(W\) is the weight of the crane; \(F_{g h}\) is the horizontal induced wind load on the girder; \(F_{s h}\) and \(F_{s v}\) are the horizontal and vertical wind load acting on the support legs respectively; and \(R_{a c}\) and \(R_{b d}\) are the reaction forces at the four wheels, \(a\), \(b\), \(c\), and \(d\).
Figure 1. Outdoor Gantry Crane and Free-Body Diagram for the Forces System.
The solution is to determine as to whether the crane will be tipping over at the center of rotation, \(R_{a c}\), due to moment on the direction of the wind induced forces. Figure 2 illustrates two cases of wind velocity, \(V = 0\) and \(V > 0\). For the given domain of \(V\), there is a reaction force, \(R_{b d}\), where in there is a resultant moment from the coplanar force system that determines the rotation of crane from the center.
Figure 2. FDB of Gantry Crane due to Effect of Wind Velocity.
Case #1 is a condition where the wind velocity is \(V = 0\). With this there will be no induced forces and the force system present on FBD are crane weight, \(W\), and the two reaction forces, \(R_{a c}\) and \(R_{b d}\), on the wheel supporting the structure. In this condition, the equilibrium for concurrent force systems is obtained by determining the equations that produce a zero resultant. The resultant will be zero and equilibrium will exist when the following equations are satisfied:
$$\sum F_x = 0 \tag{1}$$
$$\sum F_y = 0 \tag{2}$$
With the two conditions of equilibrium, reaction forces can be determined using Equation (3).
$$R_{a c} = R_{b d} = \frac{W}{2} \tag{3}$$
Case #2 is the condition wherein the wind velocity acting on the crane is inducing resultant forces that make the structure to move by rotation. In this condition, the equilibrium in terms of moment summations about the center on its line of action can be used to calculate the resultant force. Hence the two other equations of equilibrium are
$$\sum M_A = 0 \tag{4}$$
$$\sum M_B = 0 \tag{5}$$
For the case #2 on Figure 2, reaction \(R_{a c}\) is used as the center of moment. For the increasing wind velocity, \(V_{wind}\), there exist a corresponding increase in wind load represented by \(F_{g h}\), \(F_{s h}\), and \(F_{s v}\) as they are functions of wind velocity in Equation 6.
$$F_{g h} = f_{g h} (V_{wind}), \quad F_{s h} = f_{s h} (V_{wind}), \quad F_{s v} = f_{s v} (V_{wind}) \tag{6}$$
$$F_{gh} \; \uparrow , F_{s h} \; \uparrow , F_{s v} \; \uparrow \quad \text{with respect to} \quad V_{wind} \tag{7}$$
- Wind Load Analysis [3]
Wind is a mass of air that moves in a mostly horizontal direction from an area of high pressure to an area with low pressure. High winds can be very destructive because they generate pressure against the surface of a structure. The intensity of this pressure is the wind load. The wind effect is dependent upon the size and shape of the structure. Calculating wind load is necessary for the design and construction of safer, more wind-resistant building and placement of objects such as antennas on top of the buildings.
The generic formula for wind load is
$$F = A \; P \; C_d \tag{8}$$
The generic formula is used for estimating the wind load on a specific object and it does not meet the building code requirements for planning a new construction.
The formula for wind pressure, \(P\), in SI units is
$$P = \text{0.613} \; V^2 \tag{9}$$
The wind speed categorizes by the Philippine Atmospheric, Geophysical and Astronomical Services Administration (PAGASA) will be used as basis in calculation. PAGASA is the Philippine government agency responsible for providing weather forecasts, typhoon warnings, and other meteorological and astronomical services. Currently the Tropical Cyclone Wind Signal (TCWS) has been in use based on the adoption of best practices from other tropical cyclone warning centers.
The following are the corresponding wind threat based on the wind speed value.
\(C_d\) is the drag coefficient for the object subjected under wind pressure. Drag is the force that air exerts on the structure. Drag coefficient for the structure’s shape can be estimated roughly using the following standard:
- Wind Load Simulation for Gantry Crane
Figure 3 shows the effect of wind load on the gantry crane structure in terms of the equilibrium of force systems.
Figure 3. Wind Load Simulation using the Equilibrium of Force System on Gantry Crane.
The graph’s domain is based on the TCWS converted in terms of \(km/hr\). Corresponding wind speeds or velocities for the five categories of TCWS are plotted. Wheel reaction load for \(R_{b d}\) are shown for each TCWS. The red dash line which depicts \(R = 0\) is the critical wheel reaction load for \(R_{b d}\) on the FBD in Figure 2. With this \(R = 0\), the critical wind velocity is calculated to have a value of \(\text{127}\) \(km/hr\) under the TCWS #4. A horizontal wind speed which of \(V_{wind} >\) \(\text{127}\) \(km/hr\) acting perpendicularly to structure will result to tripping over the crane to the wind direction.
With this, a conclusion can be made from the simulation stated as follows: - a wind speed of over \(\text{127}\) \(km/hr\) which is within the TCWS #4 will induce an equivalent critical wind load to affect the crane stability. The use of a device in gantry crane known as “Storm Lock” is highly recommended to increase its capacity for critical wind load.
Below is the Scilab script to generate the simulation plot on Figure 3. Parameters can be edited for the other cases.
- Scilab Script
// Copyright (C) 2025 - Gani Comia // Date of creation: 24 Apr 2025 // Wind Load Effect Analysis on Outdoor Gantry Crane clear;clc; // gantry crane primary parameters for girders lG = 1.35+22+0.35; // m, crane girder length hG = 1; // m, crane girder height W = 14.5; // Tonne, crane weight shapeG = 2; // crane girder as long flat plate // gantry crane primary parameters for support legs lS = 5.7; // m, support leg length dS = 0.25; // m, support leg diameter shapeS = 1.2; // leg support as long cylinder tube // wind velocity domain Vmps = 0:52; // m/s, wind speed, tropical cyclone Vkph = Vmps*3.6; // km/hr, wind speed, tropical cyclone // modules or functions // wind load analysis using generic formula // structure surface area function A=area(l, h) // calculate girder area perpendicular to wind velocity // input argument: // l - surface length (m) // h - surface height (m) // ouput argument: // A - surface area (m^2) A = l.*h; endfunction // wind pressure function P=windPressure(V) // calculate the induced wind pressure // input argument: // V - wind velocity (m/s) // ouput argument: // P - wind pressure (N/m^2 or Pa) P = 0.613*V.^2; endfunction // drag coefficient function Cd=dragCoefficient(shape) // calculate the theortical drag coefficient // input argument: structure shape // shape = 2 for long flat plate // shape = 1.4 for shorter flat plate // shape = 1.2 for long cylinder tube // shape = 0.8 for short cylinder tube // output argument: // Cd - drag coefficient (no unit) Cd = shape; endfunction // induced wind load function Fw=windLoad(A, P, Cd) // calculate the induced wind load // input argument: // A - surface area (m^2) // P - wind pressure (N/m^2) // Cd - drag coefficient (no unit) // output argument: // Fw - wind load (N) Fw = A.*P.*Cd; endfunction // main function // wind load calculation at the girder A_g = area(lG,hG); P_g = windPressure(Vmps); Cd_g = dragCoefficient(shapeG); Fgh = windLoad(A_g,P_g,Cd_g); Fgh = Fgh/9806.65; // Tonne, wind load // wind load calculation at the support legs A_s = area(lS,dS); // m^2, surface area // angle of support leg phi = atand(((3.5/2)-0.168)/5.495); // degrees, angle Vmps_s = Vmps./cosd(phi); // m/s, wind speed perpendicular to legs P_s = windPressure(Vmps_s); Cd_s = dragCoefficient(shapeS); Fsr = windLoad(A_s,P_s,Cd_s); // force component at legs Fsh = Fsr*cosd(phi); Fsh = 3*Fsh/9806.65; // N to tonnes Fsv = Fsr*sind(phi); Fsv = 3*Fsv/9806.65; // N to tonnes // critial load Rbd = (W*(3.5/2)+Fsv*((3.5/2)+0.937)-Fgh*(6.25+0.375)-Fsh*(2.9+0.375))/3.5; // Plotting calculation results clf; fig = gcf() fig.figure_size = [700,700] plot(Vkph,Rbd,"b-","linewidth",4) note = "$\LARGE R_{wheel} = f(V_{wind})$" legend(note,with_box=%F) plot([0,200],[0,0],"r--","linewidth",1.8) title("Wind Load Effect on Outdoor Gantry Crane","fontsize",4) xlabel("Wind Velocity, Tropical Cyclone, V, (kph)","fontsize",3.5) ylabel("Wheel Reaction Load, R, (Tonne)","fontsize",3.5) xgrid(color("green"),1,7) xstring(10,0,"Critical Wheel Reaction Load = 0") xstring(120,5.0,"https://gani-mech-toolbox.blogspot.com") // Wind velocity limit of tropical cyclone Vwind = [10.8,17.2,24.5,32.7,51.3]; // m/s, wind velocity Vwind = Vwind*3.6; // kph, wind velocity // tropical cyclone signal number nVwind = length(Vwind) for i = 1:nVwind R(i) = interp1(Vkph,Rbd,Vwind(i)) vLx = [Vwind(i) Vwind(i)]; vLy = [-10 R(i)] hLx = [0 Vwind(i)]; hLy = [R(i) R(i)] plot(vLx,vLy,"k--") plot(hLx,hLy,"k--") plot(Vwind(i),R(i),"marker","d","markerFaceColor","red") xstring(Vwind(i)+8,-9.8,["Signal No. ",string(i)],-90) end // critical wind velocity format(5) Rcrit = 0 Vcrit = interp1(Rbd,Vkph,Rcrit) plot(Vcrit,Rcrit,"marker","S","markerFaceColor","red") xstring(Vcrit,Rcrit,["Critical Velocity (kph) =",string(Vcrit)])
Feel free to comment for inquiry, clarification, correction or suggestion for improvement. Drop your email to make a request to the author.
Disclaimer: The formulas and calculations
presented are for technical reference only. Users must verify the accuracy and
ensure compliance with applicable engineering standards, codes, and safety
requirements before practical application.
References
- E.A. Avallone and T. Baumeister III. Marks Standard Handbook for Mechanical Engineers. 9th Ed. McGraw-Hill International Edition. 1987.
- F.L. Singer. Engineering Mechanics. 2nd Ed. Harper International Edition, New York, Evanston & London. 1970.
- Joseph Quinones. “How to Calculate Wind Load”, last updated July 24, 2023. https://www.wikihow.com/Calculate-Wind-Load#Calculating-Wind-Load-Using-the-Generic-Formula
- “Tropical Cyclone Wind Signal.” Philippine Atmospheric, Geophysical and Astronomical Services Administration, March 23, 2022. https://www.pagasa.dost.gov.ph/learning-tools/tropical-cyclone-wind-signal