Topic: Steady-State Heat Conduction
Subject: Heat Transfer and Numerical Methods
Tool: Scilab
The steady-state heat conduction model, as represented by the Laplace equation in one dimension (1D), is the simplest partial differential equation (PDE) you may encounter solving. This equation explains the temperature characteristics or profile between the boundaries of the given domain. Presented in this article is the application of the Laplace equation in 1D using the Finite Difference Method (FDM) for the solution.
The Laplace equation in 1D for the steady-state heat conduction is shown in Equation (1).
$$\frac{\partial^2 u}{\partial x^2}\;=\;0 \tag{1}$$
The second-order PDE in 1D can also be written in ordinary differential equations (ODE). This can be approximated using the FDM shown in
Equation (2).
$$\frac{d^2 u}{d x^2}\; \approx \; \frac{u_{i+1} - 2 u_i + u_{i-1}}{\left(\Delta x\right)^2}\;=\;0 \tag{2}$$
This leads to the solution in Equation (3),
$$u_i\;=\; \frac{u_{i+1} + u_{i-1}}{2} \quad for \quad i\;=\;2,3, \ldots ,N-1 \tag{3}$$
With boundary conditions,
$$u_1\;=\;u_1, \quad u_N\;=\;u_L \tag{4}$$
Let us illustrate an example of steady-state
heat conduction as shown in Figure (1) and apply the FDM solution to understand
its temperature profile between boundaries. The Scilab script to implement the
solution will be explained in detail in relation to the Laplace equation in
1D.
The solution using the Scilab script is shown below. A short explanation
is provided for each code snippet.
Scilab Script.
clear;clc;clf;
// (1) primary & derived parameters
L = 100; // mm, length of workpiece
Nx = 11; // unit, number of nodes
dx = L / (Nx - 1); // mm, spatial stepEquation (5) is the boundary condition for this problem.
$$u_1\;=\;u_1, \quad u_{2,3, \dots ,N-1,N}\;=\;u_L \tag{5}$$
// (2) boundary temperature conditions
u = zeros(Nx, 1) + 25; // node temp cond @ 25 deg C
u(1) = 100; // boundary temperatureThe temperature condition at node points between boundaries
can be solved using the "for-end” function of the Scilab.
// (3) temperature profile at node points using FDM
for i = 2:Nx-1
u(i) = (u(i+1) + u(i-1))/2;
endBelow is the script for plotting the temperature profile.
// (4) plotting of temperature at node points
f = gcf()
f.figure_size = [600,600]
len = linspace(0,L,Nx);
plot(len, u, 'r-o');
title("Temperature Profile @ Eleven (11) Node Points","fontsize",3)
xlabel("Length, x [ mm ]","fontsize",3)
ylabel("Temperature, T [ C ]","fontsize",3)
xstring(58,73,"https://gani-mech-toolbox.blogspot.com")
eqn = ["$\LARGE \;\frac{\partial^2\,T}{\partial x^2}\,=\,0$"]
legend(eqn,with_box=%f)
xgrid(3,1)
a = gca()
a.data_bounds = [0 0; L max(u)]
a.children.children.mark_background = 9;Figure (2) is the resulting plot from executing the whole script.
The given boundary conditions in Equation (5) will result in
a curved-like temperature profile. If Equation (4) is considered as
boundary conditions with the corresponding change in primary and derived
parameters, specifically reducing the number of node points to 3, a linear
temperature profile will become the solution.
Below is the modified script for 3 node points.
// (1) primary & derived parameters
L = 100; // mm, length of workpiece
Nx = 3; // unit, number of nodes
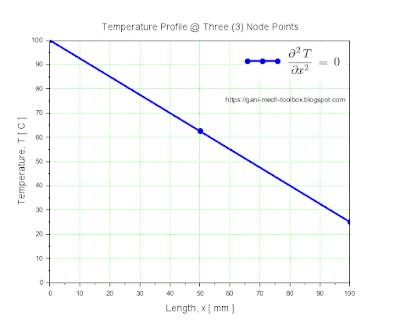
dx = L / (Nx - 1); // mm, spatial stepFigures (3) and (4) are the illustration and graphical solution
for 3 node points leading to a linear temperature profile.
The number of node points taken into consideration in solving the Laplace equation using FDM dictates the type of temperature profile, linear or curve-like. You may send a comment about the consideration for a basis as to how many node points are to be used for certain conditions of the steady-state heat conduction model.
Feel free to comment for inquiry, clarification, or suggestion for improvement. Drop your email to request the soft copy of the file.
Disclaimer: The formulas and calculations
presented are for technical reference only. Users must verify the accuracy and
ensure compliance with applicable engineering standards, codes, and safety
requirements before practical application.