Spring Simulation with Cantilever Beam Deflection Formulae using Scilab

Topic: Mechanical Spring Simulation;

Subject: Machine Design & Strength of Materials;

Tool: Scilab;

by: Gani Comia, Nov. 2024;

Beam deflection formulae of the cantilever with the concentrated load \(P\) at the free end can also be a useful tool in analyzing a mechanical spring that resembles a cantilever.

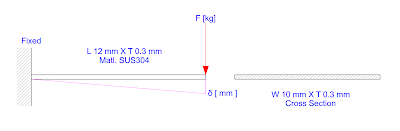
In this example, a clip spring that resembles a cantilever was simulated to determine how much load is needed to reach the maximum deflection of \(\text{0.5 mm}\). The material being considered for the application was stainless steel, \(\text{SUS304}\). Simulation also shows the deflection profile at each section of the length.

Below is a free-body diagram (FBD) of the clip spring design.

Fig.1. Clip Spring Design FBD

The following formulas for maximum deflection and deflection at any section in terms of \(x\) of the cantilever beam were applied in the analysis.

Maximum deflection.

$$\delta_{max}\;=\;\frac{P\,l^3}{3\,E\,I} \tag{1}$$

Deflection at any section in terms of \(x\).

$$y(x)\;=\;\frac{P\,x^2}{6\,E\,I}\;\left(3\,l\,-\,x\right) \tag{2}$$

Simulation using Scilab Script.

// Clip Spring Simulation
// using Cantilver Beam Deflection Formulas
// by: Gani Comia, Jul. 2017
clear;clc;

// Input:  Clip Spring Parameter
E = 806e+3;             // MPa, modulus of elasticity, SUS304
l = 12;                 // mm, length
b = 10;                 // mm, width
t = 0.3;                // mm, thickness
I = (b.*t.^3)./ 12;     // mm^4, moment of inertia

// Calculation:  Force-deflection characteristics
delta = 0.0:0.01:0.5;               // mm, deflection (allowable)
P = ((3 .*E.*I.*delta)./ l.^3);     // N, load
maxP = -max(P)                      // N, max force, downward

// Calculation: Deflection at the given length
x = 0:0.1:12;                              // mm, section length
y = (maxP.*x.^2 .* ((3*l)-x)) ./ (6*E*I);  // mm, deflection

// Visualization:
clf;
f=gcf();
f.figure_size=[600,650];

// Plot of delta vs. load
subplot(2,1,1);
plot(delta,P,"-b","linewidth",2.2);
title("Force - Deflection (SUS Clip Spring)");
xlabel("Deflection (mm)");
ylabel("Force (N)");
xstring(0.3,13.5,["Fmax:",string(max(P)),"N"]);
xgrid(12,0);

// Plot of length vs. deflection
subplot(2,1,2)
plot(x,y,"-r","linewidth",2.2);
title("Deflection - Length (SUS Clip Spring)");
xlabel("Length Segment (mm)");
ylabel("Deflection (mm)");
xgrid(12,0);

Shown is the simulation plot.

Fig. 2. Mechanical Spring as Cantilever Beam Simulation.

The Scilab simulation tool facilitates visualization of the reaction of a machine element to a given load. A machine designer might evaluate a range of attributes in their decision-making process.

Feel free to comment for inquiry, clarification, or suggestion for improvement. Drop your email to request the softcopy of the file.

Disclaimer: The formulas and calculations presented are for technical reference only. Users must verify the accuracy and ensure compliance with applicable engineering standards, codes, and safety requirements before practical application.