Topic: Mechanical Spring Simulation;
Subject: Machine Design & Strength of Materials;
Tool: Scilab;
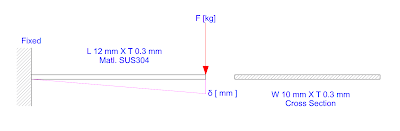
In this example, a clip spring that resembles a cantilever was simulated to determine how much load is needed to reach the maximum deflection of \(\text{0.5 mm}\). The material being considered for the application was stainless steel, \(\text{SUS304}\). Simulation also shows the deflection profile at each section of the length.
Below is a free-body diagram (FBD) of the clip spring design.
Maximum deflection.
$$\delta_{max}\;=\;\frac{P\,l^3}{3\,E\,I} \tag{1}$$
Deflection at any section in terms of \(x\).
$$y(x)\;=\;\frac{P\,x^2}{6\,E\,I}\;\left(3\,l\,-\,x\right) \tag{2}$$
Simulation using Scilab Script.
// Clip Spring Simulation // using Cantilver Beam Deflection Formulas // by: Gani Comia, Jul. 2017 clear;clc; // Input: Clip Spring Parameter E = 806e+3; // MPa, modulus of elasticity, SUS304 l = 12; // mm, length b = 10; // mm, width t = 0.3; // mm, thickness I = (b.*t.^3)./ 12; // mm^4, moment of inertia // Calculation: Force-deflection characteristics delta = 0.0:0.01:0.5; // mm, deflection (allowable) P = ((3 .*E.*I.*delta)./ l.^3); // N, load maxP = -max(P) // N, max force, downward // Calculation: Deflection at the given length x = 0:0.1:12; // mm, section length y = (maxP.*x.^2 .* ((3*l)-x)) ./ (6*E*I); // mm, deflection // Visualization: clf; f=gcf(); f.figure_size=[600,650]; // Plot of delta vs. load subplot(2,1,1); plot(delta,P,"-b","linewidth",2.2); title("Force - Deflection (SUS Clip Spring)"); xlabel("Deflection (mm)"); ylabel("Force (N)"); xstring(0.3,13.5,["Fmax:",string(max(P)),"N"]); xgrid(12,0); // Plot of length vs. deflection subplot(2,1,2) plot(x,y,"-r","linewidth",2.2); title("Deflection - Length (SUS Clip Spring)"); xlabel("Length Segment (mm)"); ylabel("Deflection (mm)"); xgrid(12,0);
Shown is the simulation plot.
The Scilab simulation tool facilitates visualization of the reaction of a machine element to a given load. A machine designer might evaluate a range of attributes in their decision-making process.
Feel free to comment for inquiry, clarification, or suggestion for improvement. Drop your email to request the softcopy of the file.
Disclaimer: The formulas and calculations presented are for technical reference only. Users must verify the accuracy and ensure compliance with applicable engineering standards, codes, and safety requirements before practical application.