Spring Simulation with Cantilever Beam Deflection Formulae using Scilab

Topic: Mechanical Spring Simulation;

Subject: Machine Design & Strength of Materials;

Tool: Scilab;

by: Gani Comia, Nov. 2024;

Beam deflection formulae of the cantilever with the concentrated load \(P\) at the free end can also be a useful tool in analyzing a mechanical spring that resembles a cantilever.

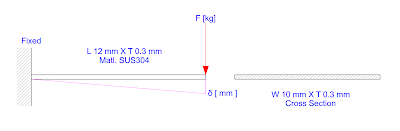
In this example, a clip spring that resembles a cantilever was simulated to determine how much load is needed to reach the maximum deflection of \(\text{0.5 mm}\). The material being considered for the application was stainless steel, \(\text{SUS304}\). Simulation also shows the deflection profile at each section of the length.

Below is a free-body diagram (FBD) of the clip spring design.

Fig.1. Clip Spring Design FBD

The following formulas for maximum deflection and deflection at any section in terms of \(x\) of the cantilever beam were applied in the analysis.

Maximum deflection.

$$\delta_{max}\;=\;\frac{P\,l^3}{3\,E\,I} \tag{1}$$

Deflection at any section in terms of \(x\).

$$y(x)\;=\;\frac{P\,x^2}{6\,E\,I}\;\left(3\,l\,-\,x\right) \tag{2}$$

Simulation using Scilab Script.

// Clip Spring Simulation
// using Cantilver Beam Deflection Formulas
// by: Gani Comia, Jul. 2017
clear;clc;

// Input:  Clip Spring Parameter
E = 806e+3;             // MPa, modulus of elasticity, SUS304
l = 12;                 // mm, length
b = 10;                 // mm, width
t = 0.3;                // mm, thickness
I = (b.*t.^3)./ 12;     // mm^4, moment of inertia

// Calculation:  Force-deflection characteristics
delta = 0.0:0.01:0.5;               // mm, deflection (allowable)
P = ((3 .*E.*I.*delta)./ l.^3);     // N, load
maxP = -max(P)                      // N, max force, downward

// Calculation: Deflection at the given length
x = 0:0.1:12;                              // mm, section length
y = (maxP.*x.^2 .* ((3*l)-x)) ./ (6*E*I);  // mm, deflection

// Visualization:
clf;
f=gcf();
f.figure_size=[600,650];

// Plot of delta vs. load
subplot(2,1,1);
plot(delta,P,"-b","linewidth",2.2);
title("Force - Deflection (SUS Clip Spring)");
xlabel("Deflection (mm)");
ylabel("Force (N)");
xstring(0.3,13.5,["Fmax:",string(max(P)),"N"]);
xgrid(12,0);

// Plot of length vs. deflection
subplot(2,1,2)
plot(x,y,"-r","linewidth",2.2);
title("Deflection - Length (SUS Clip Spring)");
xlabel("Length Segment (mm)");
ylabel("Deflection (mm)");
xgrid(12,0);

Shown is the simulation plot.

Fig. 2. Mechanical Spring as Cantilever Beam Simulation.

The Scilab simulation tool facilitates visualization of the reaction of a machine element to a given load. A machine designer might evaluate a range of attributes in their decision-making process.

Feel free to comment for inquiry, clarification, or suggestion for improvement. Drop your email to request the softcopy of the file.

Disclaimer: The formulas and calculations presented are for technical reference only. Users must verify the accuracy and ensure compliance with applicable engineering standards, codes, and safety requirements before practical application.

Plotting Position, Velocity & Acceleration as a function of Time

Topic: Position, Velocity & Acceleration Plot as a Function of Time

Subject: Numerical Methods & Kinematics

Tool: Scilab

by: Gani Comia, Nov. 2024

In the subject of kinematics, the position, velocity, and acceleration as a function of time can be plotted using the forward difference of the numerical method of differentiation. For a given position as a function of time, t, as represented by s = f(t), velocity and acceleration can be solved as s' = f'(t) and s'' = f''(t), respectively.

The Scilab "diff()" function facilitates the numerical differentiation of a given function.

Below is an example of a Scilab script to make a plot of position, velocity, and acceleration as a function of time.

Scilab Script.

// Copyright (C) 2024 - Gani Comia
// Date of creation: 21 Nov. 2024
// Position, Velocity & Acceleration as a function of time
clear;clc;
// Given: Position as a function of time, t.
// s(t)=3t^4 - 35t^3 + 120t^2 - 10

function s=f(t)
    s = 3*t.^4 - 35*t.^3 + 120*t.^2 - 10
endfunction

dt = 0.01                   // time step, dt
t = 0:dt:5                  // time range, t
s = f(t)                    // position, s
v = diff(s)/dt              // velocity, ds/dt (s')
a = diff(s,2)/dt.^2         // acceleration, d2s/dt2 (s'')

clf;
f = gcf()
f.figure_size = [600,700]

// position vs time plot
subplot(3,1,1)
plot(t,s,"-r","linewidth",2.5)
title_1=["Position ,", "$s=3\;t^4-35\;t^3+120\;t^2-10$"]
title(title_1, "fontsize",3)
ylabel("position, s")
xgrid()

// velocity vs time plot
subplot(3,1,2)
plot(t(1:$-1),v,"-b","linewidth",2.5)
title_2=["Velocity ,", "${ds}\;/\;{dt}$"]
title(title_2,"fontsize",3)
ylabel("velocity, v")
xgrid()

// acceleration vs time plot
subplot(3,1,3)
plot(t(1:$-2),a,"-g","linewidth",2.5)
title_3=["Acceleration ,", "${d^2s}\;/\;{dt^2}$"]
title(title_3,"fontsize",3)
ylabel("acceleration, a")
xlabel("time, t","fontsize",2)
xgrid()

Below is the graph as a result of running the Scilab script.

Fig. 1. Graph of Position, Velocity & Acceleration as a function of Time. 
Feel free to comment for inquiry, clarification, or suggestion for improvement. Drop your email to request the soft copy of the file.
Disclaimer: The formulas and calculations
presented are for technical reference only. Users must verify the accuracy and
ensure compliance with applicable engineering standards, codes, and safety
requirements before practical application.

Pumps Total Dynamic Head (TDH) and Pressure using EMT

Topic: Visual Plot of Pump's Pressure Head and Volumetric Flow;

Subject: Fluid Mechanics;

Tool: Euler Math Toolbox;

by: Gani Comia, Nov. 2024;

In one scenario, a 100 GPM volumetric flow of water is being required in a building's fire protection system. Your facility manager is asking if it can be achieved from existing < 70 GPM and if the pressure setting can be adjusted from the current 100 psi to something like 160 psi. As a technical resource person in mechanical, you need to provide an explanation with the supporting calculation and visual simulation in layman's terms.

EMT Script

Pumps Total Dynamic Head & Pressure

The pump's horsepower (HP) is calculated from a given volumetric flow rate (Q) of fluid and the total dynamic head (H):

HP=QH1714e

To determine the total dynamic head (TDH), H:

Solution:

>HP = 10+2.5;         // hp, e.g. fire pump + jockey pump
>Q  = 50:120;         // gpm, volumetric flow from 50 to 100
>e  = 0.80;           // %, efficiency (assumed)
>H  = (1714*HP*e/Q);  // ft, total dynamic head

Pressure head calculation:

P=γh

where:

>gamma = 62.4;        // lb/ft^3, weight density of H2O
>h = H;               // ft, pressure head
>P = (gamma*h)/144;   // psi (from lb/ft^2), pump pressure

Data Visualization:

>aspect(1);
>plot2d(P,Q,title="Fire & Booster Pump Characteristic", ...
 xl="Pump Pressure [psi]",yl="Pump Vol. Flow [gpm]");

Shown in fig. 1. is plot generated by EMT script.

Fig. 1. Visual representation of the pump's characteristics.

Feel free to comment for inquiry, clarification, or suggestion for improvement. Drop your email to request the softcopy of the file.

Disclaimer: The formulas and calculations presented are for technical reference only. Users must verify the accuracy and ensure compliance with applicable engineering standards, codes, and safety requirements before practical application.