Shaft-Hub Assembly Press or Shrink Fit Axial Force and Torque

Topic: Thick-Wall Theory for Cylinders

Subject: Machine Design

Tools: Scilab and QCAD

By: Gani Comia, Feb. 2025

• Interfacial or Contact Pressure

The contact pressure in a press or shrink fit of the shaft and hub assembly due to interference fit is used to calculated the axial force to disassemble the hub in the direction of the shaft. Likewise, it is used to calculate the torque to rotate the hub around the shaft axis as well. Figure 1 shows the forces and torque in a shaft-hub assembly of machine elements.

Figure 1. Pressure, Force, and Torque in the Shaft-Hub Assembly

This article presents the equations for calculating interfacial pressure between the surface of the shaft and the hub and apply it to solve for axial force and torque. Let us define and illustrate the problem using Figure 2.

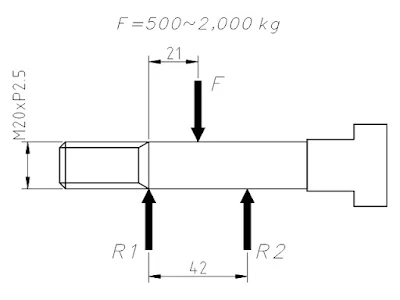
Figure 2. Sample Shaft-Hub Assembly and Parameters

The contact pressure, \(p\), between the internal surface of the hub and outer surface of the shaft can be expressed as a function of interference as shown in Equation (1).

$$p = \left[ \frac{1}{K_h + K_s} \right] \frac{\delta_{total}}{R} \tag{1}$$

Where:
\(K_h\) – constant for outside member or the hub
\(K_s\) – constant for inside member or the shaft
\(\delta_{total}\) – total radial interference
\(R\) – mean radius at the interface of contacting surface

The constants for the outside (hub) and inside (shaft) members are defined as,

$$K_h = \frac{1}{E_h} [C_h + \nu_h], \quad C_h = \frac{\zeta_h^2 + 1}{\zeta_h^2 - 1}, \quad \zeta_h = \frac{r_h}{R} \tag{2}$$

$$K_s = \frac{1}{E_s} [C_s - \nu_s], \quad C_s = \frac{\zeta_s^2 + 1}{\zeta_s^2 - 1}, \quad \zeta_s = \frac{R}{r_s} \tag{3}$$

For the solid shaft where the inside radius is

$$r_s = 0 , \quad \zeta_s = \frac{R}{r_s} = \infty , \quad C_s = 1 \tag{4}$$

Then the constant for the inside member or the shaft becomes,

$$K_s = \frac{1}{E_s} [1 - \nu_s] \tag{5}$$

Where:
\(E_h\) and \(E_s\) – modulus of elasticity of the hub and shaft respectively
\(\nu_h\) and \(\nu_s\) – Poisson ratio of the hub and shaft respectively
\(r_h\) – outside radius of the hub
\(r_s\) – inside radius of the shaft
\(\zeta_h\) and \(\zeta_s\) – ratio of the radius defined in Equations (2) and (3)
\(C_h\) and \(C_s\) – geometric constant

• Radial Force

$$F_r = 2 \pi R L p \tag{6}$$

Where:
\(F_r\) – radial force
\(L\) – length of contact

• Tangential Force

$$F_t = f F_r \tag{7}$$

Where:
\(F_t\) – tangential force

• Torque

$$T = 2 \pi R^2 L f p \tag{8}$$

Where:
\(T\) – torque
\(f\) – coefficient of static friction

Below is the application of the equations presented to calculate for the solution of the illustrated problem with the use of Scilab script.

• Scilab Script

// Copyright (C) 2025 - Gani Comia
// Date of creation: 28 Feb 2025
// Shaft-Hub Press or Shrink Fit Assembly Calculation
clear;clc;
// (1) --- methods or functions ---
// (1-1) interfacial pressure between shaft-hub assembly
function p=cP(Kh, Ks, radInt, R)
    p = (1/(Kh+Ks)).*(radInt./R);
endfunction

// (1-2) hub, K-constant
function Kh=kHconst(E_h, nu_h, r_h, R)
    zeta = r_h./R;
    C_h = (zeta.^2 + 1)./(zeta.^2 - 1);
    Kh = (1/E_h).*(C_h + nu_h);
endfunction

// (1-3) shaft, K-constant
function Ks=kSconst(E_s, nu_s)
    C_s = 1;
    Ks = (1/E_s).*(C_s - nu_s);
endfunction

// (1-4) radial force due to interfacial pressure
function fRad=radialF(p, R, L)
    fRad = p.*2*%pi.*R.*L./9.8;
endfunction

// (1-5) tangential force due to radial force
function fTan=tangentF(f, fRad)
    fTan = f.*fRad;
endfunction

// (1-6) torque at interference surface
function T=torque(fTan, R)
    T = fTan.*R./1000;
endfunction

// (2) --- main function ---
// (3) hub parameters, steel with the following properties
id_h = [50.280 50.300];     // mm, hub ID
od_h = 100.0;               // mm, hub OD
or_h = od_h./2;             // mm, hub outside rad         
E_h = 213e3;                // MPa (N/mm^2), modulus of elasticity
nu_h = 0.295;               // poisson ratio
L =  25.0;                  // mm, length of contact
f = 0.1;            // coefficient of static friction steel-to-steel

// (4) shaft parameter, steel with the following properties
od_s = [50.350 50.370];     // mm, shaft OD
id_s = 0;                   // mm, shaft ID
E_s = 205e3;                // MPa (N/mm^2), modulus of elasticity
nu_s = 0.28;                // poisson ratio

// (5) derived parameters
format(7);
// (5-1) mean radius at the interface
R = (1/2)*[(od_s(1)+id_h(2))/2 , (od_s(2)+id_h(1))/2];
// (5-2) total radial interference
radInt = (1/2)*[(od_s(1)-id_h(2)) , (od_s(2)-id_h(1))];
// (5-3) diametral interference
diaInt = 2*radInt;
mprintf("Dia Inter (mm): min:%4.3f & max:%4.3f\n",diaInt(1),diaInt(2));

// (6) calculation
for i = 1:2
    Kh(i) = kHconst(E_h,nu_h,or_h,R(i));
    Ks(i) = kSconst(E_s,nu_s);   
    p(i) = cP(Kh(i),Ks(i),radInt(i),R(i));
    fRad(i) = radialF(p(i),R(i),L);
    fTan(i) = tangentF(f,fRad(i));
    T(i) = torque(fTan(i),R(i));
end

mprintf("Axial Force (kgf): min:%5.0f & max:%5.0f\n",fTan(1),fTan(2));
mprintf("Torque (kgf-m): min:%4.0f & max:%4.0f\n",T(1),T(2));

// (7) plot calculation results
clf;
fig = gcf()
fig.figure_size = [800,600]

subplot(1,2,1);

// (7-1) Fa = f(delta) relationship 
m_a = diff(fTan)/diff(diaInt);
b_a = fTan(1) - m_a.*diaInt(1);
x_a = linspace(0.040,0.100,50);
y_a = m_a.*x_a + b_a;

// (7-2) plot of axial force - diametral interference
plot(x_a,y_a,"b-","linewidth",3);
title(["$\Large Fa = f(\delta)$","for","$\Large f_s=0.1$"],"fontsize",3.5);
xlabel(["$\large \delta$",", Dia Interference, mm"],"fontsize",3.25)
ylabel(["$\large Fa$",", Axial Force, kgf"],"fontsize",3.25);
xgrid(3,0);
mprintf("Line Prop: m=%6.1f and b=%3.1e\n",m_a,b_a);
legend("$\LARGE F_a = 62726.3\;\delta$",with_box=%F);
xstring(0.045,7000,"https://gani-mech-toolbox.blogspot.com");
ax = gca()
ax.data_bounds = [0.040 2000; 0.100 8000];

format(6)
// (7-3) axial force @ min diametral interference
for j = 1:2
    v_x = [diaInt(j) diaInt(j)]; v_y = [2000 fTan(j)];
    plot(v_x,v_y,"m--","linewidth",1.5);
    h_x = [0.04 diaInt(j)]; h_y = [fTan(j) fTan(j)];
    plot(h_x,h_y,"m--","linewidth",1.5);
    plot(diaInt(j),fTan(j),"s","markerFaceColor","magenta");
    xstring(diaInt(j)-0.001,fTan(j),["Fa = ",string(fTan(j))],-40);
end

subplot(1,2,2);

// (7-4) T = f(delta) relation ship
m_t = diff(T)/diff(diaInt);
b_t = T(1) - m_t.*diaInt(1);
x_t = linspace(0.040,0.100,50);
y_t = m_t.*x_t + b_t;

// (7-5) plot of torque - diametral interference
plot(x_t,y_t,"r-","linewidth",3);
title(["$\Large T = f(\delta)$","for","$\Large f_s=0.1$"],"fontsize",3.5);
xlabel(["$\large \delta$",", Dia Interference, mm"],"fontsize",3.25);
ylabel(["$\large T$",", Torque, kgf-m"],"fontsize",3.25);
xgrid(3,0);
ax = gca()
ax.data_bounds = [0.040 60; 0.100 180];
mprintf("Line Prop: m=%6.1f and b=%3.1e\n",m_t,b_t);
legend("$\LARGE T = 1578.4\;\delta$",with_box=%F);
xstring(0.045,160,"https://gani-mech-toolbox.blogspot.com");

format(5);
// (7-6) torque @ min & max diametral interference
for k = 1:2
    v_x = [diaInt(k) diaInt(k)]; v_y = [60 T(k)];
    plot(v_x,v_y,"m--","linewidth",1.5);
    h_x = [0.04 diaInt(k)]; h_y = [T(k) T(k)];
    plot(h_x,h_y,"m--","linewidth",1.5);
    plot(diaInt(k),T(k),"s","markerFaceColor","magenta");
    xstring(diaInt(k)-0.001,T(k),["T = ",string(T(k))],-42);
end

• Scilab Output (Figure 3)

Figure 3. Axial Force and Torque in relation to Diametral Interference

For the cylinder to be considered to follow the thick-walled theory, the ratio of thickness over diameter should be \(t\,/\,D > 0.1\), giving rise to tangential and radial stresses within the wall.

It is encouraged the reader to refer to the book Mechanical Engineering Design, 7th edition text by Joseph Edward Shigley, Charles R. Mischke and Richard G. Budynas for the detailed discussion of the subject.

Feel free to comment for inquiry, clarification, or suggestion for improvement. Drop your email to request the soft copy of the file. 

Reference

1. J.E. Shigley, C.R. Mischke, and R. Budynas. Mechanical Engineering Design. 7th Ed. McGraw-Hill Publishing Company. 2003.

Optimization of Cylindrical Container Design at Minimum Material Cost

Topic: Functional Model and Graphs
Subject: Calculus
Tool: Scilab

By: Gani Comia, Feb. 2025

This article demonstrates the use of Scilab in solving a simple optimization problem for the calculation of a cylindrical container’s radius, \( \mathbf{r} \), and height, \( \mathbf{h} \), at the minimum material cost. Let us illustrate an example problem with the following given values and figures.

Cylindrical Container

Volume: \(24 \pi\)  cubic inch

Cost of Material at Top and Bottom: \( \text{PHP 3.00}\) per square inch

Cost of Material at Curved Side: \( \text{PHP 2.00} \) per square inch

Figure 1. Cylindrical Container Drawing

For optimal cost, there is a size of cylindrical container in terms of the combination of radius and height that will bring the material cost at a minimum. This problem needs a derivation of the function model for the material cost in terms of radius. The total material cost in making the container can be expressed in Equation (1).

$$C = 2 C_{tb} A_{tb} + C_{cs} A_{cs} \tag{1}$$

Where:

\(C\) – total material cost, PHP

\(C_{tb}\) – cost at top and bottom cap per unit area, PHP/sq.in.

\(A_{tb}\) – material area at top and bottom cap, sq.in.

\(C_{cs}\) – cost at the curved side per unit area, PHP/sq.in.

\(A_{cs}\) – material area at the curved side, sq.in.

$$A_{tb} = \pi r^2 , \quad C_{tb} = 3 \tag{2}$$

$$A_{cs} = 2 \pi r h , \quad C_{cs} = 2 \tag{3}$$

Where:

\(r\) – radius of the cylindrical container, in.

\(h\) – height of the cylindrical container, in.

Substituting Equations (2) and (3) to (1),

$$C = 2(3)(\pi r^2) + 2(2\pi r h) \tag{4}$$

$$C = 6 \pi r^2 + 4 \pi r h \tag{5}$$

The above cost function should be expressed using one independent variable, as in this case radius, \(r\). For the given volume, \(V\), we can find the relationship between \(r\) and \(h\).

$$V = \pi r^2 h \tag{6}$$

$$24 \pi = \pi r^2 h \quad \text{or} \quad h = \frac{24}{r^2} \tag{7}$$

By substituting \(h\) from Equation (7) to (5), the total material cost \(C\) can be rewritten in Equation (8).

$$C(r) = 6 \pi r^2 + \frac{96 \pi}{r} \tag{8}$$

Equation (8) can be the functional model to determine the value of radius, \(r\), for the minimum material cost, \(C(r)\). The solution can be found with the use of Scilab functions of finding the minimum value of the cost, \( \mathbf{min()}\), and \( \mathbf{interp1()}\), to find the radius using interpolation.

Scilab Script

// Copyright (C) 2025 - Gani Comia
// Date of creation: 13 Feb 2025
// Cylindrical Container Design at Minimum Material Cost
clear;clc;

// (1) derived functional model
function C=f(r)
    C = 6*%pi.*r.^2 + 96*%pi./r;
endfunction

// (2) domain and range of the function
r = 0.5:0.1:4;
C = f(r);

// (3) plot of the function
clf;
plot(r,C,"linewidth",3);
note1 = "Material Cost for Cylindrical Container Design";
title(note1,"fontsize",3.5);
xlabel("Radius [inch]","fontsize",3.5);
ylabel("Material Cost [PHP]", "fontsize",3.5);
xgrid(3,0);
legend("$\LARGE C(r)=6\,\pi\,r^2\;+\;\frac{96\,\pi}{r}$",with_box=%F);
xstring(2.4,550,"https://gani-mech-toolbox.blogspot.com");

// (4) interpolated value of radius and minimum cost
cost = min(C);
disp(cost);
radius = interp1(C,r,cost);
disp(radius);
xVer = [radius radius]; yVer = [150 cost];
plot(xVer,yVer,"r--","linewidth",1.75);
xHor = [0.5 radius]; yHor = [cost cost]
plot(xHor,yHor,"r--","linewidth",1.85);
plot(radius,cost,"marker","s","markerFaceColor","blue");
format(7);
note2 = ["Min Cost (PHP):", string(cost); "Radius (in.): ", string(radius)];
xstring(radius-0.1,cost+20,note2);

Scilab Output (Figure 2)

Figure 2. Plot of Material Cost Function for Cylindrical Container

After solving the radius, \(r\), the height, \(h\), of the cylindrical container can be computed using Equation (7). The solution is shown in Equation (9).

$$h = \frac{24}{r^2} = \frac{24}{2^2} = 6 \; \text{in.} \tag{9}$$

An alternative method to solve for the minimum, \(r\), is by derivation of the cost function, \(C(r)\), and setting its derivative to zero to solve for \(r\). 

Feel free to comment for inquiry, clarification, or suggestion for improvement. Drop your email to request the soft copy of the file. 

Factor-of-Safety using Yield Stress and Maximum Shear Stress Theory

Topic: Steady Loading and Failure Theory

Subject: Machine Design

Tool: Scilab

By: Gani Comia, Feb. 2025

A static or steady load is a stationary force or moment acting on a machine or structural member. There are two approaches to calculate the margin of safety to prevent failures on the member: - factor-of-safety (\({FoS}\)) and reliability approach. These examine or compare the strength of a member and the anticipated induced stress from static loading for the selection of the optimum or suitable material and dimensions.

This article demonstrates the use of \({FoS}\) approach in verifying the suitability of a machine member for the given steady load. Figure 1 illustrates the condition in which the T-bolt made of AISI 1050 will be used as shackle pin to carry or lift a range of steady load from 500 to 2000 kg. The \(FoS\) approach can determine the maximum dead load the pin is capable of lifting steadily.

Figure 1. Shackle pin subjected to a steady loading.

Equations (1), (2), and (4) represent the basis for calculating \({FoS}\) from the given condition.

\({FoS}\) in Simple Tension, Compression, or Bending

$${FoS}_{bending}\;=\;\frac{\sigma_{yp}}{\sigma_{max}} \tag{1}$$

Where:
\({FoS}_{bending}\) – factor-of-safety in simple tension, compression, or bending
\(\sigma_{yp}\) – material’s yield point
\(\sigma_{max}\) – maximum induced stress

\({FoS}\) in Pure Shear

$${FoS}_{shear}\;=\;\frac{\tau_{yp}}{\tau_{max}} \tag{2}$$

Where:
\({FoS}_{shear}\) – factor-of-safety in pure shear
\(\tau_{yp}\) – material’s yield point in shear
\(\tau_{max}\) – maximum induced shear stress

\({FoS}\) using Max Shear Stress Theory

$$\tau_{mss}\;=\;\sqrt{\left(\frac{\sigma_{max}-\sigma_{min}}{2}\right)^2 + \tau_{max}^2} \tag{3}$$

$${FoS}_{mss}\;=\;\frac{\tau_{yp}}{\tau_{mss}} \tag{4}$$

Where:
\({FoS}_{mss}\) – factor-of-safety based on maximum shear stress theory
\(\tau_{mss}\) – induced stress using max shear stress theory
\(\sigma_{max}\) – stress due to bending at outermost surface of the shackle pin
\(\sigma_{min}\) – stress due to bending at neutral axis of the shackle pin

For steady loading, the recommended factor-of-safety is from 1.5 to 3.0 for the general engineering applications and ductile materials. The use of 1.5 as factor-of-safety will determine the maximum allowable steady load for a member. Presented below is the Scilab script for calculation documentation and validation of design in a typical engineering organizational setup.

Scilab Script

// Copyright (C) 2025 - Gani Comia
// Date of creation: 7 Feb 2025
// Shackle Pin Stress Analysis Rev 01
clear;clc;

// (1) Primary and secondary parameters.
d = 17.5;               // mm, minor dia for M20 thread
L = 42.0;               // mm, length under load
Wt = 500:10:2000;       // kg, weight of load
F = Wt.*9.8;            // N, load per pin
A = (%pi/4)*d.^2;       // mm^2, cross-sectional area at thread
S = (%pi/32)*d.^3;      // mm^3, section modulus of pin

// (2) Maximum moment and shear load.
Mmax = F.*L./4;         // N-mm, max moment load
V = F./2;               // N, max shear load

// (3) Bending and shear stress.
sigmaMax = Mmax./S;     // MPa, max bending stress
tauMax = (4/3)*V./A;    // MPa, max shear stress

// (4) Material properties, AISI 1050
sigmaYp = 375.0;        // MPa, yield point
tauYp = 0.5*sigmaYp;    // MPa, yield point in shear

// (5) Factor-of-safety (FoS), Bending and Pure Shear
FoSbending = sigmaYp./sigmaMax;     // factor-of-safety in bending
FoSshear = tauYp./tauMax;           // factor-of-safety in pure shear

// (6) Factor-of-safety (Fos), Max Shear Stress Theory
sigma1 = sigmaMax;          // MPa, max principal stress, outermost
sigma3 = 0;                 // MPa, min principla stress, neutral axis
tauMss = sqrt(((sigma1-sigma3)/2).^2 + tauMax.^2);  // MPa, MSST
FoSmsst = tauYp./tauMss;    // factor-of-safety in max shear stress

// (7) Plot of analysis
clf;
plot("ln",Wt,FoSmsst,"b-","linewidth",3);
plot("ln",Wt,FoSbending,"r--","linewidth",1.5);
plot("ln",Wt,FoSshear,"m-","linewidth",2.5);
note1 = ["Max Shear Stress","Bending Stress","Shear Stress"];
legend(note1,with_box=%F);
xgrid(3,0);
title("Shackle Pin FoS based on Failure Theory","fontsize",3.5);
xlabel("Lifting Load [kg]","fontsize",3);
ylabel("Factor of Safety","fontsize",3);

// Interpolating weight for the min factor-of-safety 1.5
format(6);
fos = 1.5;
wtInt = interp1(FoSmsst,Wt,fos);
disp(fos, wtInt);
xVerMin = [wtInt wtInt]; xHorMin = [400 wtInt];
yVerMin = [0 fos]; yHorMin = [fos fos]; 
plot(xVerMin, yVerMin,"b--");
plot(xHorMin, yHorMin,"b--");
plot(wtInt, fos,"marker","s","markerFaceColor","blue");
note2 = ["Max Load (kg) =",string(wtInt),"@ FoS =",string(fos)];
xstring(wtInt-50,fos+0.4,note2);
note3 = "https://gani-mech-toolbox.blogspot.com";
xstring(1200,11,note3);

Scilab Script Output (Figure 2)

Figure 2. Plot of Calculation of the Three Failure Theories.

The resulted plot shows that for a minimum factor-of-safety of 1.5, the shackle pin should only be loaded with not more than 1232 kg to prevent failure. 

Just like any engineering drawings to document the mechanical design, calculation in the form of scripts and notebooks are also kept for design review and future reference.

Feel free to comment for inquiry, clarification, or suggestion for improvement. Drop your email to request the soft copy of the file.